안녕하세요
너무 궁금해서 조언을 구하고 싶습니다.
군 간 비교 때 쓰는 독립 t- test 나 세군 이상 비교시 쓸때 anova 돌릴때 궁금증이 생깁니다.
예를 들어 두 군(A, B)에서 A군에게는 "ㄱ", B군에게는 "ㄴ" 이라는 중재를 하여 두 군중 어느 군이 더 많은 근력 증가가 있는지 알고자 합니다
 ?
?
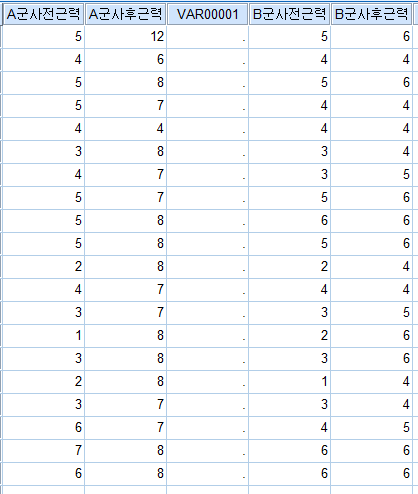
위 처럼 코딩을 하였습니다. A, B 군 모두 사전데이터는 정규분포 하였습니다. A, B군의 사전데이터 동질성을 검정하기 위해 독립 t-test를 실시해보니

?이렇게 나왔습니다. 즉, "사전데이터는 두군간 차이가 없다"? 그래서 두 군간 비교를 하기 위해선 사전데이터가 동질하다는 가정하에 위 통계 코딩의 "A군사후근력"과 "B군사후근력" 즉, 중재 후 데이터 값들만 가지고 군간 비교를 해도 괜찮은지요?
이때 만약 사후 근력 데이터가 정규분포를 하지 않는다면 비모수 방법의 통계를 써야하나요? 사전 데이터는 정규분포를 하였는데...
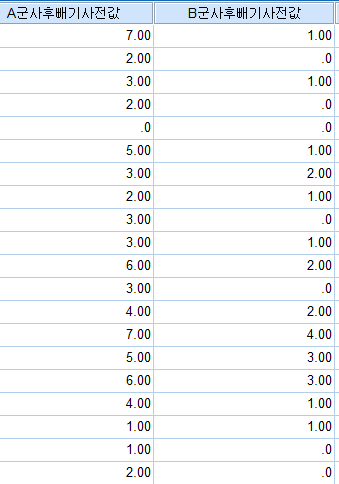
만약 위 방법같은 군간 비교가 안된다면 위 그림 처럼 A군사후-A군사전="A군변화값", B군사후-B군사전="B군변화값" ? 데이터를 따로 만들고 정규분포 한지 알아보고 모수 비모수 통계법을 사용하여 두 군간 비교를 실시하여야 하는지요?
그리고 군내 변화를 알아 볼때 사전 근력은 정규분포 만족 사후 근력 데이터는 정규분포 불만족 이렇게 나오면 모수 모수 방법인 paired t-test를 사용해야 하는지 아니면 비모수 방법인 Wilcoxon signed rank test ?를 사용해야 하는지요?
한가지 더 위에 나타난 사전데이터 독립 t-test가 만약 군간 차이가 있다고 나타나면 즉, 처음 데이터가 차이가 있다고 나오면 출발점이 서로 틀리기 때문에 위에서 제시한 post-pre의 difference 값(변화량)을 가지고 군간 비교를 할 수 있는지요?
정말 죄송합니다. 아무리 인터넷을 보고 책을 뒤져보아두 알수가 없어서 이렇게 어렵게 메일을 보냅니다.
통계돌린땐 새로 생성된 데이터는 무조건 정규성분포 검사를 하여 모수 비모수 통계법을 따라야 하나요? 아니면 위 처럼 사전 데이터만 정규분포하다면 사후 데이터는 그냥 모수법을 따라가도 되는지요?
조언 부탁드립니다.